Swift幂运算

在 Swift 中，幂运算（Power） 主要通过使用 pow 函数来完成，但 Swift 并不支持使用 ^ 作为幂运算符（^ 在 Swift 中是按位异或操作）。

使用 pow 进行幂运算

import Foundation

let result = pow(2.0, 3.0) // 2 的 3 次方
print(result) // 输出 8.0

注意： pow 返回的是 Double 类型，如果需要其他类型，可以进行类型转换。

let resultInt = Int(pow(2.0, 3.0)) // 转成 Int
print(resultInt) // 输出 8

自定义幂运算运算符（**）

如果希望使用更方便的运算符，例如 **，可以自定义一个运算符：

import Foundation

infix operator **: MultiplicationPrecedence

// 定义 `**` 运算符
func ** (base: Double, exponent: Double) -> Double {
    return pow(base, exponent)
}

// 也可以为 Int 类型扩展
func ** (base: Int, exponent: Int) -> Int {
    return Int(pow(Double(base), Double(exponent)))
}

// 示例
let doubleResult = 2.0 ** 3.0
print(doubleResult) // 输出 8.0

let intResult = 3 ** 4
print(intResult) // 输出 81

快速幂运算（递归实现）

如果需要更高效的整数幂运算，可以使用快速幂算法：

func fastPower(_ base: Int, _ exponent: Int) -> Int {
    if exponent == 0 {
        return 1
    }
    let half = fastPower(base, exponent / 2)
    if exponent % 2 == 0 {
        return half * half
    } else {
        return half * half * base
    }
}

// 示例
print(fastPower(2, 10)) // 输出 1024

详细推算：

第一次调用：fastPower(2, 10)，exponent = 10，half = fastPower(2, 10 / 2)。

第二次调用：fastPower(2, 5)，exponent = 5，half = fastPower(2, 5 / 2)，5 / 2 = 2（整数除法向下取整）。

第三次调用：fastPower(2, 2)，exponent = 2，half = fastPower(2, 2 / 2)。

第四次调用：fastPower(2, 1)，exponent = 1，half = fastPower(2, 1 / 2)，1 / 2 = 0（整数除法向下取整）。

第五次调用：fastPower(2, 0)，exponent = 0，half = fastPower(2, 0)，直接返回1。

从最底层往上计算：

fastPower(2, 0) = 1

fastPower(2, 1) = 1 * 1 * 2 = 2

fastPower(2, 2) = 2 * 2 = 4

fastPower(2, 5) = 4 * 4 * 2 = 32

fastPower(2, 10) = 32 * 32 = 1024

奇偶性不同的问题：

if exponent % 2 == 0 {
    return half * half
} else {
    return half * half * base
}

奇偶性之所以不同，是因为指数分解时，幂运算的性质导致不同情况需要不同处理。

如果 exponent 是偶数，可以直接拆成两个相同的幂相乘，比如 2^10：

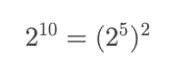
我们可以直接把 10 一分为二，变成 5，递归计算 2^5，然后将结果平方即可。

但如果 exponent 是奇数，直接对 exponent / 2 取整，会丢失一个 base，所以要额外乘以 base，比如 2^5：

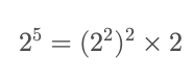
5 不能直接一分为二得到整数，所以要写成 5 = 2 \times 2 + 1。

这就意味着：多出来一个 base，需要额外乘上 base。

所以 2^5 其实是 2^4 之后再乘以一个 2。

Swift 幂运算的常见用法

1、计算平方、立方：

let square = pow(4.0, 2.0) // 4 的平方
let cube = pow(3.0, 3.0)   // 3 的立方
print(square, cube) // 16.0 27.0

2、计算平方根：

let squareRoot = pow(9.0, 0.5)
print(squareRoot) // 输出 3.0

3、负指数（取倒数）：

let inverse = pow(2.0, -1.0)
print(inverse) // 输出 0.5