要理解为什么使用 cos 和 sin 来计算角度和坐标,需要从数学上的圆和三角函数的关系说起。
圆的基本特性
1、在一个以原点为圆心、半径为 r 的圆上,任何一点的位置都可以用极坐标表示:
点的位置由角度(用弧度或度数表示)和半径决定。
极坐标可以转化为平面上的直角坐标系(即 x 和 y 坐标)。
2、对于某个角度 θ:
点的 x 坐标 = 圆心的 x 坐标 + 半径 × cos(θ)
点的 y 坐标 = 圆心的 y 坐标 + 半径 × sin(θ)
这背后的原因在于三角函数的定义。
三角函数的定义
三角函数(sin 和 cos)描述的是一个角度对应的 x 和 y 的比值关系:
1、假设我们在一个单位圆上(半径为 1,圆心在原点)。
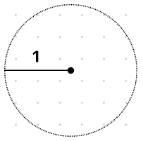
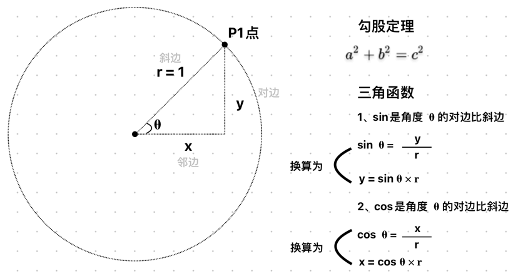
2、对于角度 θ,它对应单位圆上的一个点:
x 坐标是点到 y 轴的水平距离:cos(θ) 。
y 坐标是点到 x 轴的垂直距离:sin(θ) 。
如果圆的半径是 r,那么点的坐标会被放大到:
x = r × cos(θ)
y = r × sin(θ)
为什么用 cos 和 sin 来计算坐标
在 SwiftUI 中,视图的位置是在二维平面(x 和 y 坐标)上确定的。
1、圆形排列的需求
我们希望将子视图均匀分布在一个圆上。
坐标必须依据每个点的角度(angle)动态计算。
2、通过三角函数确定坐标
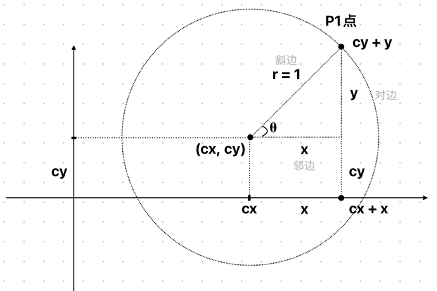
假设圆的半径为 r,圆心的坐标为 (cx, cy),一个点的角度为 θ:
水平偏移量:r × cos(θ),表示从圆心水平向外的距离。
垂直偏移量:r × sin(θ),表示从圆心垂直向外的距离。
点的坐标:
x = cx + r × cos(θ)
y = cy + r × sin(θ)
3、计算多个点的坐标
如果需要将 n 个子视图均匀分布在圆上,每个子视图的角度可以计算为:

或用弧度表示:
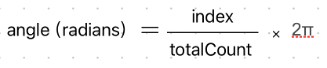
每个角度都可以用 cos 和 sin 转换为坐标。
举例:点在圆周上的坐标
圆的参数
圆心:(150, 150)
半径:100
点的数量:4
每点的角度间隔:360° ÷ 4 = 90°
计算每个点的坐标
点 0:角度 0°
x = 150 + 100 × cos(0) = 150 + 100 = 250
y = 150 + 100 × sin(0) = 150 + 0 = 150
点 1:角度 90°
x = 150 + 100 × cos(90°) = 150 + 0 = 150
y = 150 + 100 × sin(90°) = 150 + 100 = 250
点 2:角度 180°
x = 150 + 100 × cos(180°) = 150 – 100 = 50
y = 150 + 100 × sin(180°) = 150 + 0 = 150
点 3:角度 270°
x = 150 + 100 × cos(270°) = 150 + 0 = 150
y = 150 + 100 × sin(270°) = 150 – 100 = 50
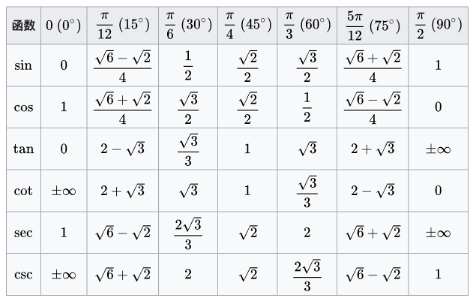
图片来源:三角函数
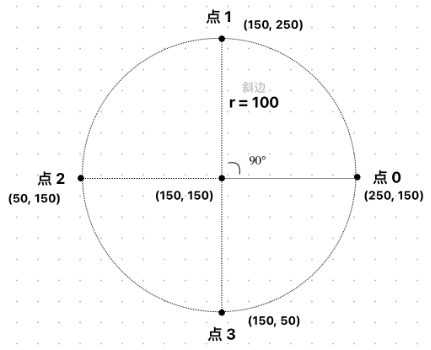
最终四个点的坐标分别是:
(250, 150)
(150, 250)
(50, 150)
(150, 50)
这些点均匀分布在以 (150, 150) 为圆心、半径为 100 的圆上。
使用 cos 和 sin 的关键总结
三角函数本质:cos 和 sin 是用角度计算圆周上点的水平和垂直偏移的工具。
圆形布局:通过三角函数,可以将角度轻松转换为平面坐标。
均匀分布:子视图通过不同的角度(index)均匀排列,坐标动态计算。



